Fuere

Verso fuori.

Categoria: Informatica Pagina 1 di 4

How to set program-specific icon theme on KDE Plasma 5

Di

il 18 Febbraio 2018

in Informatica

Cari amici,
dopo un pomeriggio speso a cercare la soluzione di un banale e fastidioso problema col mio calcolatore, e non avendone trovata alcuna in rete, ho deciso di riportare quella che ho scovato qui sul blog. Anni or sono Fuere ospitava spesso articoli a carattere informatico, ma la mia vena “nerd” si è esaurita da tempo, quando iniziai a usare intensamente il computer per l’Università e il lavoro. L’articolo è stato scritto in lingua inglese, affichè il massimo numero di internauti possa fruirne. Come al solito, ho cercato di dargli un tono un po’ ironico e polemico : spero risulti perlomeno divertente anche ai non interessati.

 

This post describes how to set an application to use a particular icon theme (different from the default one) in KDE Plasma 5, while leaving other programs use the default one.

I can already hear purists bleathering: “Why do you want two icon themes at once in your installation? You should use an unique icon theme! It has to be consistent! Otherwise it’s not elegant!”. Let me answer them the short way: go to hell. If I learned something in my Physics studies, it is: “The world is complicated”. It’s truly more complicated than you can thing about, and the number of points of view is simply infinite. If I like my computer to use two icon sets at the same time, why should I care something about what others say elegance is? Who told them what beauty is? Did they dig this out of themselves, or are they mindless repeating what their favourite guru said, as with religious principles? In fact they are just imaginationless coformists.

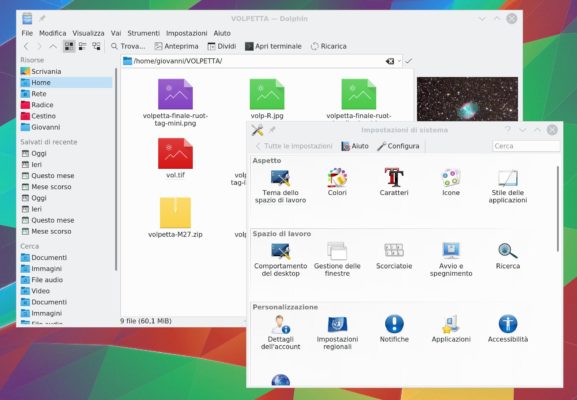
Dolphin with “Breeze” and System-settings with “Oxygen” icon theme

I’ve always found myself happy with the old default “Oxygen” icon theme in KDE. On the other hand, I cannot stand the new “Breeze” one: it’s way too simplified. A program which I use almost everyday, the “Kstars” virtual planetarium, recently stopped shipping it’s own icons and included them in the standard Breeze distribution. The icons themselves are stupidly black and white, just the opposite of what an icon should be to be easiliy spotted among the others. They call it “material design”, I would call it “idiocy made by Google”. As a result of merging the icons into Breeze, under Oxygen almost all icons in the program were absent, making it almost impossible to use.

I searched in the Internet for two hours for a solution: there were multiple articles describing how to change the icon of a program in the start menu, some on how to set a new global icon theme, but none was saying how to change the theme inside one single specific application. I started to suspect that such a functionality did not exist. Fortunately, I was wrong.

In order to do the trick, you have first to locate the directory in which your KDE rc-files are located. This is usually “~/.config”, but you can find it out using this command:

kf5-config –path config

Inside the path, there sould be a “kdeglobals” file, which specifies global settings for all KDE applications. If you have a look in it, you will see a block like this:

[Icons]

Theme=Oxygen

This instruction sets the icon theme of your KDE environment. In order to make it application-dependent, you have to enter a similar block in the rc file of the program whose icons you want to change. In my case, I switched kstars only to use Breeze icons (black and white icons are better than nothing), by putting inside the file “kstarsrc” the following:

[Icons]

Theme=Breeze

Log-out from your desktop and log-in again, et voilá! Kstars now uses Breeze, while the rest of the system still relies on Oxygen. You can change the icons of all your applications, if you want, and then send a screenshots to the simpler-is-better-church followers to watch them perish in green flames!!

Allineamento immagini solari

Di

il 29 Maggio 2016

in Astrofotografia, Immagini astronomiche, Informatica

Il 9 maggio scorso il tempo sull’Italia settentrionale era pessimo: era in transito una perturbazione di provenienza atlantica e sulle prealpi la copertura nuvolosa era pressoché totale. Per riuscire a vedere il transito di Mercurio, un fenomeno relativamente raro che consiste nel passaggio del piccolo pianeta davanti al Sole, ho fatto una breve gita in Germania, valicando le Alpi e sorpassando le nuvole in volata. Appena finirò di elaborare le immagini pubblicherò un resoconto dell’escursione.

Tornato a casa, si è posto il problema di come utilizzare il materiale raccolto. Mi sono concentrato su un breve video, della durata di 8 minuti circa, che riprendeva Mercurio mentre passava vicino a un gruppo di macchie solari. Il filmato era stato girato alla velocità di 50 fotogrammi al secondo, ma ciascuno di essi era disturbato dalla turbolenza atmosferica, che impediva di scorgere i dettagli dell’inquadratura. In casi come questo di solito si mediano più fotogrammi per ottenerne uno solo, in cui gli effetti di distorsione sono ridotti. Per fare ciò bisogna che tutti i fotogrammi siano prima riallineati nel modo più preciso possibile.

L’allineamento delle fotografie astronomiche che riprendono campi stellari è relativamente semplice: bisogna far corrispondere le immagini delle stelle in un’immagine alle immagini delle stesse stelle di un’altra. Con delle foto della superficie solare ad alto ingrandimento, la scarsità e la variabilità dei dettagli rendono l’operazione più difficile. Cercando in rete ho trovato un algoritmo generico abbastanza semplice che può essere d’aiuto. Funziona così: di ciascuna immagine si calcola la trasformata di Fourier bidimensionale discreta \mathcal{I}_i(\vec{k}\,) e si costruisce lo spettro di potenza incrociato:

{\rm P}_{i,j}(\vec{k}\,)\,=\,\mathcal{I}_i(\vec{k}\,)\cdot\mathcal{I}_j^{\mbox{*}}(\vec{k}\,)

Qui \vec{k}\,=\,(k_x,\,k_y) è il momento associato a \vec{r}\,=\,(x,\,y) che descrive le immagini bidimensionali.
Così come lo spettro di potenza di un segnale è la trasformata della funzione di autocorrelazione, si può mostrare che lo spettro di potenza incrociato è la trasformata della funzione di correlazione incrociata (o cross-correlazione):

{\rm R}_{i,j}(\vec{r}\,)\,=\,\mathcal{F}^{-1}\big[ {\rm P}_{i,j}(\vec{k}\,) \big]

Quando uno ha per le mani la funzione di correlazione incrociata “er ist fertig”, almeno in teoria. Infatti, in linea di principio, se le due immagini fossero l’una la traslazione rigida dell’altra la cross-correlazione avrebbe un picco di intensità alle coordinate corrispondenti al vettore di traslazione. In altre parole, quando si ha la cross-correlazione si sa di quanto spostare la seconda immagine per allinearla alla prima.

Tradurre in una tecnica pratica i risultati di qualche calcolo non è mai un’operazione immediata. Per allineare i fotogrammi ho scritto uno script in Python (potete scaricarlo al termine dell’articolo) che include questi passaggi:
 

  1. Le immagini sono ridotte in bianco e nero e la scala dei colori è invertita, in modo che il dettaglio più evidente (il disco di Mercurio) risulti molto luminoso su uno sfondo scuro. Le due immagini da allineare sono ricampionate alla metà della loro dimensione originaria (bin 2×2), per ridurre gli effetti della turbolenza.
  2. A ciascuna viene applicata una maschera gaussiana con 4px di sigma per distruggere eventuali difetti puntuali dell’immagine. Si trova il massimo d’intensità delle due immagini. Questo corrisponde pressapoco al centro del disco di Mercurio (X,Y).
  3. Attorno alle coordinate (2X,2Y) di ciascuna immagine originale (non ricampionata) si ritaglia un quadrato di 128 pixel per lato. Questa misura è comoda perché è una potenza di 2 ed è sufficiente, nel mio caso, a contenere l’intero Mercurio. Dei due quadrati si trova la funzione di correlazione incrociata, come descritto in precedenza.
  4. La funzione di cross-correlazione può essere interpretata essa stessa come un’immagine quadrata di dimensione 128×128 pixel. Se ne trovano le coordinate del massimo assoluto e tali valori sono usati per far partire un fit gaussiano del picco d’intensità, che fornisce la posizione del massimo con precisione sub-pixel (x,y).
  5. L’immagine originale è traslata della quantità non intera (-2X-x,-2Y-y) e ricampionata alla griglia dei pixel della prima immagine interpolandola con una spline cubica.

 

Schemata informativa di "Flecken"

La schermata informativa del programma “Flecken”. Con una scala di colori modificata, sono visibili l’immagine di referenza, quella da allineare, l’immagine di cross-correlazione col contorno del fit gaussiano.

 

È finita? Certamente no, a questo punto bisogna suddividere i fotogrammi in gruppi omogenei e mediarli. Chiaramente ciascun gruppo di fotogrammi non può contenerne più di un certo numero, perché col tempo che passa il pianeta si sposta! Nel mio caso i fotogrammi erano 24018 e li ho suddivisi in gruppi da 250 l’uno, ottenendo 96 immagini finali mediate. La media è stata fatta con una funzione che pure avevo scritto in precedenza e che fa parte di una minuscola libreria in Python dove ho raccolto un po’ di operazioni utili per manipolare le immagini, gcim.

Alla fine del circo, l’algoritmo di allineamento ha riallineato tutti i 24018 fotogrammi: in 5 casi (0,02% del totale) il fit gaussiano non è andato a buon fine e si è usata una traslazione con precisione al pixel intero; in 66 casi (0,27% del totale) il fit gaussiano è converso ad un valore abnorme, probabilmente a causa di un gradiente lineare sottostante al picco gaussiano. L’identificazione di questi 66 casi è stata possibile grazie al registro dove lo script salva tutti i dettagli di cosa fa. Sto ancora pensando a un modo per permettergli di riconoscere automaticamente questi casi.
 

Confronto fotogrammi

Confronto tra due fotogrammi non allineati. Il pianeta e le macchie solari sono in posizioni diverse.

Confronto fotogrammi allineati

Confronto tra i fotogrammi precedenti dopo l’allineamento. Il pianeta è ora fisso nella stessa posizione.

 

Alla fine ho usato un programma libero, ImPPg (che pure, volendo, implementa una procedura simile per l’allineamento delle immagini) per applicare dei filtri di deconvoluzione alle immagini risultanti. Ho quindi rimontato un piccolo video accelerato, che aggiungerò presto su questo sito.

Infine, ecco lo script di allineamento: ne ho prodotto due versioni, rispettivamente “Fleck” e “Flecken”. Il primo allinea due immagini, salvando una versione traslata della seconda per farla coincidere con la prima. Il secondo fa la stessa cosa ma in modo sequenziale, lavorando su una lista di immagini da allineare. Per eseguirli avete bisogno di un’installazione di Python con i moduli Numpy, Scipy, Matplotlib. Serve anche la mia piccola libreria gcim, che è già inclusa assieme agli script. Potete scaricare tutto da qui.

Francamente, dubito che il programma, così com’è, possa servire a qualcuno per allineare le sue immagini. Non so nemmeno come si comporti con dei fotogrammi diversi da quelli del video per il quale l’ho scritto. Ma di certo può essere un buon punto di partenza, se qualcuno ha voglia di lavorarci un po’ su.

A presto!

Inversione delle serie di potenze

Di

il 29 Dicembre 2015

in Fisica, Informatica, Matematica

Oggi torno, dopo un lungo periodo, a discutere di un argomento puramente teorico. Recentemente, un problema posto dal mio amico L mi ha portato a considerare la possibilità di invertire una serie di potenze. In altre parole, data una funzione espressa come serie di potenze in x, si vorrebbe un metodo per trovare la serie di potenze che definisce la sua inversa:

f(x)=\sum_{n=1}^{+\infty}f_n x^n\qquad\qquad g(x)=\sum_{n=1}^{+\infty}g_n x^n

g\circ f(x) = g(f(x)) = \sum_{i=1}^{+\infty}g_i \bigg({\sum_{j=1}^{+\infty}f_j x^j}\bigg)^i = x

Il problema è di una certa rilevanza poiché spesso le inverse non sono facilmente esprimibili in termini di funzioni “semplici” come quelle di partenza. Ad esempio, se si considera:

y = f(x) = x + \sin(x)

Si noterà subito che non esiste un numero finito di passaggi per trovare x in funzione di y. In effetti, tale relazione è un’equazione trascendente ed è il fulcro del problema posto dal mio amico: a lui serviva un’espressione approssimata per l’inversa, in modo da non dover ricorrere ogni volta ad un procedimento numerico per trovare una soluzione.

Ci sono molti modi per venirne a capo. Nutrendo ancora (nonostante i cinque anni di sofferenza) una passione segreta per la matematica, ho probabilmente seguito quello più teorico e avulso dalla realtà, l’unico vantaggio del quale è la sicurezza che esso tende, con l’aumentare della precisione, alla vera inversa. Naturalmente non è nulla di nuovo, cercando ben bene qualcosa in internet l’avevo pure trovato, ma scritto in modo tanto formale da risultare incomprensibile (e per queste parole mi perdoni C, un altro mio amico).

L’idea è di scrivere la funzione come serie di potenze e di determinare dai suoi coefficienti quelli dell’inversa. Dopo una giornata di conti, sono riuscito a trovare le relazioni che definiscono i coefficienti dell’inversa fino al settimo grado; per andare oltre, ho dovuto scrivere una piccola libreria in Python e metterla a punto per due giorni. Le prime relazioni sono:

{g_1} = \frac{1}{f_1}
g_2 = -\frac{f_2}{f_1^3}
g_3 = \frac{2f_2^2}{f_1^5} - \frac{f_3}{f_1^4}

Oltre alla prima, piuttosto ovvia, per ottenerle bisogna pareggiare i termini di grado uguale nello sviluppo della doppia sommatoria di cui sopra. Ciò conduce al problema delle partizioni degli interi (dove l’intero da partizionare è l’esponente del grado considerato) e alla loro rappresentazione tramite i diagrammi di Young o di Ferres. È chiaro dalle relazioni che esse valgono solo se la funzione “diretta” ha derivata diversa da zero sul punto dove è sviluppata, altrimenti l’inversa ha derivata divergente sullo stesso punto e lo sviluppo in serie di potenze intere cessa di essere possibile.

Ho scritto un breve documento dove delineo il procedimento teorico per ottenere le relazioni e risolvo il problema di x+sin(x). Potete accedervi da qui: Inversione di Serie di Potenze. Mi raccomando, non passate tutto il giorno a invertire serie di potenze, può far molto male. Non dite che non vi avevo avvertiti!

A presto!

Pagina 1 di 4

Successivo

Powered by WordPress & Tema di Anders Norén